
This method enable people to investigate very large sparse matrices (10000 by 10000 with 50 non-zero elements on each column) in a matter of hours on a workstation. Unfortunately, the author recently learned about a so-called maximum entropy or moment method which is perhaps even faster (but we are yet doubtful about its theoretical origin, see Papers on probability, statistics and statistical physics by E. T. Jaynes). This project is part of the effort to see whether another enhancement in the order of ten is possible, due to the fact that this method is very simple and should be easy to parallelize.
As shown in the paper, the main computational cost of the algorithm is in sparse matrix -- vector products, of the form:
u4=u4-A*u2
where u4, u2 are vectors and A is a square matrix,
both being complex. In f77 it can be written as,
do i=1,n3
do k=1,idx(i)
u4(id(k,i)) = u4(id(k,i))-A(k,i)*u2(i)
enddo
enddo
where idx(i) is the number of non-zero elements on the
ith column of A, and id(k,i) would be the
row indices of those elements, ranging from 1 to n3 ,
n3 usually is a very big number in the order of 10^5.A very simple solution would be to write a HPF program and turn it to the compiler. But there isn't any HPF compiler on xolas machines. It is also do-able by just calling Petsc subroutines, and indeed by the native Blas2 layer it may well be the fastest implementation on a single processor. However for inter-processor communications Petsc uses MPI, which is OK for processors linked by shared memory (in PS#1, the benchmark for throughput on Xolas is 400 Mbits/s in MPI shared memory mode compared to about 10 Mbits/s in MPI distributed memory mode for inter-processor communications), but apparantly not the best -- what actually happens is still data being copied, only in shared memory it doesn't take any time to send the data, compared to using TCP/IP in distributed memory communications. Also, we would like to try our own luck in parallelizing a code and to feel the "pain", which lead us to the following.
First, we realized that f77 would not be able to handle the entire task by itself, the reason being that all memory allocations in the main program must be done at compiler stage, thus all memory pointers are fixed numbers (except for those passed from external subroutines) in the binaries. Thus it would be impossible to dynamically allocate a piece of (shared) memory for it. There is an option in shmat which seems to indicate that you can attach a shared memory segment to a logical address unused by the system . But wherever your fortran program is loaded that piece of the logical address will be mark "used" by the system, and invariably an "unable to attach shared memory segment" error message will appear if you try to attach an allocated segment of shared memory to it.
On the other hand, the serial version was written in f77 and it would be too much work to convert every code you have in fortran to C by hand just to use shared memory. It is also quite impossible to use machine converters like f2c, once you see what it generates. And f77 is more efficient and simpler to use for complex number operations, although it is true that, for simple multiplications, the gap is diminished after you use good compiler options like "-fast -xO5". See test.c and test.f.
We did hybrid coding in C and Fortran. Shared memory allocation, management and process control is done using C program shm.c, but the computational part is done by passing shared memory pointers to fortran subroutines. This way we affected minimal changes to the original Fortran program (see mulcp.F). For multiple processes, we used UNIX system call fork , which can be directly used in fortran:
C Fork the program here: resources such as idx(i), id(k,i) and
C A(i,j) (read only) will be automatically "cloned".
Master_pid = getpid()
My_pid = Master_pid
Master_idx = 1
My_idx = Master_idx
do i=2,num_processors
if (My_pid.eq.Master_pid) then
call fork
My_pid = getpid()
if (My_pid.ne.Master_pid) My_idx = i
endif
enddo
C slave processors: wait here
if (My_pid.ne.Master_pid) then
call slave_wait_for_command (My_idx)
call exit()
endif
We used a master-slave mechanism with simple coordination protocols,
through an array called schedule_flags in the shared
memory. Each slave owns one byte in schedule_flags.
volatile char *schedule_flags; #define U_TO_U2 1 #define U2_TO_U4 2 #define U4_TO_U6 3 #define U6_TO_U8 4 #define U8_TO_U10 5 #define COLLECT_MY_DOMAIN_TO_U2 11 #define COLLECT_MY_DOMAIN_TO_U4 12 #define COLLECT_MY_DOMAIN_TO_U6 13 #define COLLECT_MY_DOMAIN_TO_U8 14 #define COLLECT_MY_DOMAIN_TO_U10 15 #define TRANSFER_FROM_V 21 #define TRANSFER_TO_V 22 #define SLAVE_DIE 99The slave processes always reside in the following subroutine after being created:
void slave_wait_for_command_ (int *My_idx) {
double *in, *out;
extern void f77_sparse_multiply_ (double*,double*,int*,int*);
while (1)
{
/* My_idx is from 1 to num_processors */
switch(schedule_flags[*My_idx-1])
{
...
case U2_TO_U4: in=u2;
/* my part is: */
out = copy+(*My_idx-1)*size_of_vector_in_double;
/* clear the work space region */
memset (out,0,size_of_vector_in_bytes);
/* operate in the range indicated by layout_ */
f77_sparse_multiply_ (in,out,&domain[2*(*My_idx)-2],
&domain[2*(*My_idx)-1]);
/* NOT schedule_flag to show that it's done. */
schedule_flags[*My_idx-1] = ~schedule_flags[*My_idx-1];
break;
...
}
}
}
Only the master process passes through the main loop of the program mulcp.F. Whenever it meets some time
consuming computation, it first sets schedule_flags to
activate the slave processes, then does his own share defined in
layout_, and then check if all the slaves are done. A slave
process signifies he is finished by ~ (NOT) his flag.
void watch_slaves (char what)
{
int i;
char sum;
while(1)
{
sum = ~what;
for (i=1;i < layout_.num_processors;i++)
{
sum &= schedule_flags[i];
}
if (sum==~what) return;
}
}
void master_multiply (char what)
{
...
/* send command to all slaves */
memset(schedule_flags,what,sizeof(char)*layout_.num_processors);
/* works out his own share (good master) */
switch(what)
{
...
case U2_TO_U4: in=u2; goto there;
...
there: memset (copy,0,size_of_vector_in_bytes);
f77_sparse_multiply_ (in,copy,domain,domain+1);
...
}
/* check how the slaves are doing */
watch_slaves(what);
/* if the slaves are done: collect the copies */
...
}
It is imperative to declare the "schedule_flags" as volatile, which tells the compiler to execute the loops in watch_slaves() as intended. Otherwise the compiler might decide that since there is no explicit data dependecy in the loop it might as well execute only once.
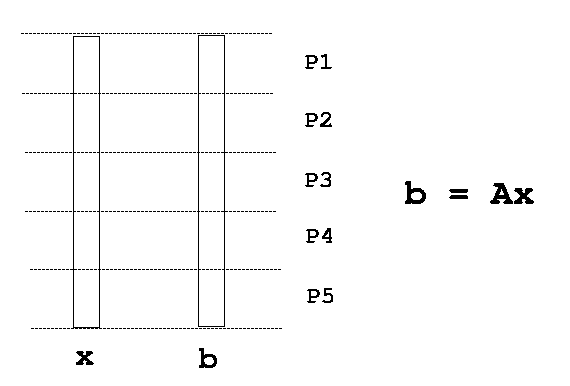
COMMON /LAYOUT/ num_processors, domain(2*MAX_PROCESSORS)
INTEGER num_processors, domain
...
n3avg = n3/num_processors
do i=1,num_processors
domain(i*2-1) = 1+(i-1)*n3avg
domain(i*2) = domain(i*2-1)+n3avg-1
enddo
domain(num_processors*2) = n3
C allocate shared memory for everything:
if (generate_shm_block(n3,num_processors).eq.0) then
print*,'Error in allocating shared memory: Check if there is'
print*,'any undeleted shared memory allocation from previous run.'
stop
endif
...
and linked with C (shm.c) declaration
/* link with fortran common block "layout" */
extern struct
{
int num_processors;
int domain;
} layout_ ;
int *domain = &layout_.domain;
In order to ensure data integrity, some kind of protection should be
employed when different processes accumulate to the same piece of
shared memory, such as
mutex. However we found such approaches to be far too
expensive for sparse matrix-vector products. We adopted a simpler
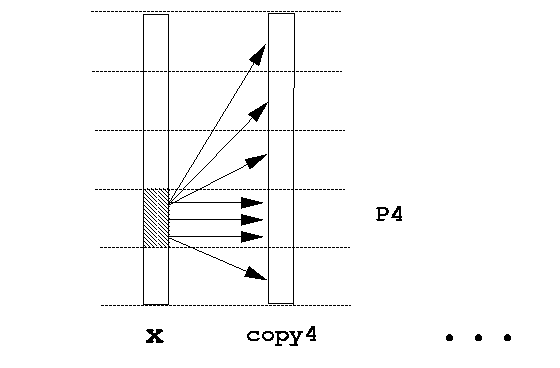
method: each processor multiplies (or scatters) his own
part into seperate copies and in the end add the copies
together. The procedure is best explained by the following graphs:
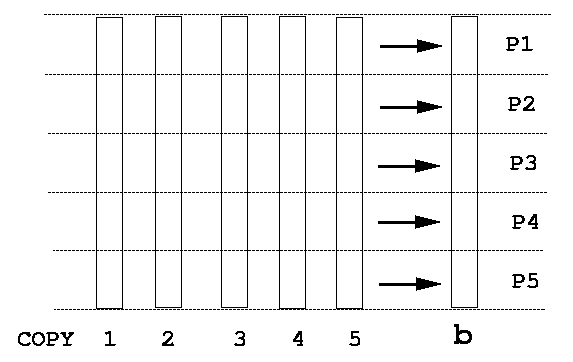
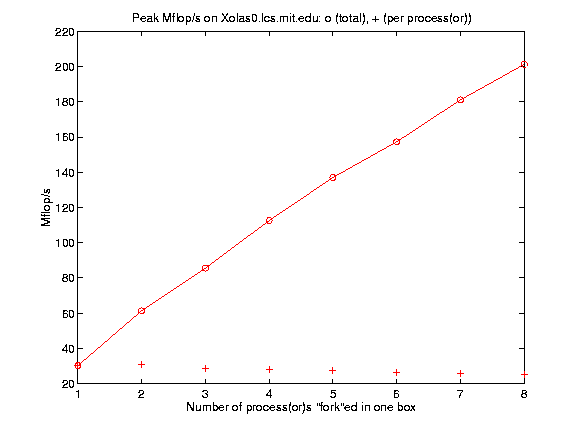
As can be predicted, such a parallel programming style could extract the most out of a given algorithm on shared memory machines. Very little overhead in process control is involved, so linear scaling of computational speed with the number of processors is expected. This is confirmed by the figure: